前進オイラー法

時間

時間を\( t \)と記述することにします。
時計を見たときを、現時刻\( t_{n} \)とし、
\[ t=t_{n} \]
と記録しておくことにします。
次に時計をみる時刻は\( dt \)経過後とします。
その時刻を\( t=t_{n+1} \)として記録すると、
\[ t_{n+1}=t_{n}+dt \]
という関係式が得られます。
\( dt \)間隔で記録をすることにすれば、
\[ t_{n+2}=t_{n+1}+dt =t_{n} + 2 dt \]
という関係があることがわかります。

記録開始時点の時刻を\( t_0=0 \)と決めると、
\[ t_1 = t_{0} + dt \]
\[ t_2 = t_{1} + dt \]
\[ \dots \]
\[ t_{n-1} = t_{n-2} +dt \]
\[ t_{n} = t_{n-1} + dt \]
となり、各時刻の数値が確定します。
つまり、記録する時間の増え方（時間増分）が\( dt \)で一定であるとすると、
ある時刻が既知である場合、その時刻に時間増分を足せば、次の時刻が求まる
という関係になっていることがわかります。
時刻の値が必要な場合には、記録開始時を原点に定めれば、すべての\( n \)に対して時刻の値が
確定することもわかります。

時間を決める常微分方程式

それでは、時間を常微分方程式（ODE: Ordinary Differential Equations)で記述してみましょう。
それは、
\[ dt/dt=1 \]
と書けます。
\( t \)はその時間変化が\( dt/dt=1 \)となるようなものであるという意味です。
この式を差分で書いてみると、
\[ [t_{n+1}-t_{n} ]/dt = 1 \]
となり、
\[ t_{n+1} = t_{n} + dt \]
という式が出てきます。これは先ほど示した関係式と一致します。
このことから、時間\( t \)に関する常微分方程式は、
\( dt \)後の状態　= 現時刻の状態　＋　増分
の関係を決めるものだということがわかります。

状態を決める常微分方程式

今度は\( y \)を時間の関数として、
\[ dy(t)/dt = -y (t) \]
というODEを考えます。
この式をみると、この式の解\( y(t) \)は、現時刻の\( y(t) \)に\( － \)をつけた量に等しい変化率\( dy(t)/dt \)をもつような\( y(t) \)であることを示しています。
先ほどと同じ論法を使うと、\( dt \)が小さいとき、
\[ [y(t_{n+1})-y(t_{n})]/dt = – y(t_{n}) \]
と書けると思ってください。
すると、
\[ y(t_{n+1}) = y(t_{n}) +(-y(t_{n})) dt \]
という式が得られます。
式の形をわかりやすくするために、
\[ y_{n} = y(t_{n}) \]
\[ y_{n+1} = y(t_{n+1}) ] \]
と書くことにすると、上の式は、
\[ y_{n+1} – y_{n} = (-y_{n}) dt \]
となります。
時間の場合は、ODEの右辺が\( １ \)であったので見えなかったのですが、
今回は右辺が\( -y \)であるので、増分＝変化率×時間幅　という形が
はっきりと見えました。

Eulerの前進解法

それでは、一般的なODEである
\[ dy/dt = f(y,t) \]
の場合はどのように書けるかというと、
\[ y_{n+1} – y_{n} = f(y_{n}, t_{n})dt \]
となります。
この方法は、現時刻の状態から未来を決める方法であり、
オイラーの前進解法（Forward Euler Algorithm)
と呼ばれているものです。オイラーの陽解法（Explicit Euler’s method)とも呼ばれています。

解析解

オイラーの前進解法が妥当かどうかを確認してみます。
そのために、
\[ dy/dt= – y \]
の解析解(Analytic solution)を求めます。
\( y \)の始まりの状態を決めないと数値が決まらないのは時間の場合と同じですので、
\[ t_{0} = 0 \]
\[ y_{0} =y(t_{0}) = 1 \]
とします。
これを初期条件（Initial condition）と言います。
\( dy/dt=-y \)の両辺を\( y \)でわると、
\[ (1/y)dy/dt = -1 \]
両辺を時間\( t \)について\( [0,t] \)まで積分すると、\( C_{1} \)を任意定数として、
\[ \log y = -t + C_{1} \]
となります。
これから、
\[ y(t) = \exp (-t+C_{1})=\exp (C_{1}) \exp (-t) \]
これに、初期条件を入れてやると、
\[１＝\exp (C_{1}) \]
と決まります。
従って、解析解は
\[ y(t) = \exp (-t) \]
となります。皆さんは電卓をもってきて、調べたい時間\( t \)を\(0.1 \)といった具合に
指数関数\( \exp \)に入力すれば、\( y(0.1)= \exp (-0.1)=0.9048 \)といった数値であることがわかります。

Pythonによる数値計算

では、Pythonを使って、解析解とオイラー前進解法による数値計算之結果を比較してみましょう。
数値で評価する方法もありますが、グラフィックスを使って、解析解と数値的に求めた値が一致するかどうかを確認する方法が便利です。

結果は下図の通りです。実線が解析解、記号をつけたものがオイラー前進解法による数値計算の結果です。両者はよく一致しています。

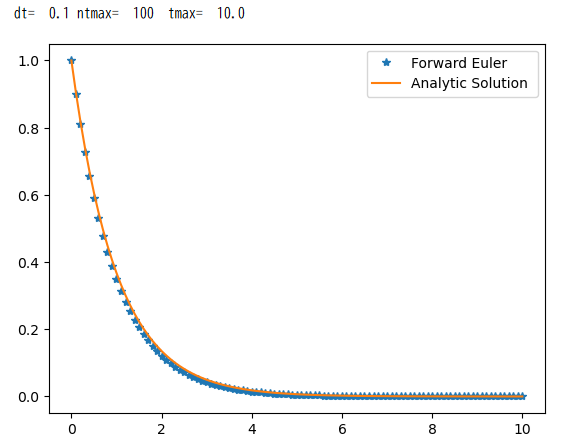
皆さんは\( dt \)をどの程度大きくすると解析解との差が生じるか、確認をしてみてください。

いま、皆さんは道の上を歩いているとします。現在の地点からある地点まで進もうとするとき、皆さんはいま歩いている速度\( v_{n} \)を調べて、\(１ \)秒後にはその速度×\( １ \)秒に相当する距離だけ移動できると考えます。これはオイラーの前進解法に基づいた予測です。
ある地点に正確に到達するには\(１\)秒後を考えるよりは\( 0.1 \)後の移動距離を考えながら進んだ方が目指す地点により精度よく到達できることはすぐにわかります。
\( x_{n+1}=x_{n} + v_{n} dt \)　の形の推測を使う場合には、\( dt \)はある程度小さくとる必要があるというのはなんとなく理解していただけるでしょう。