水平投げ出しとアニメーション

ボール（質点とみなせると仮定）を地上から\( 1 \) mの高さから水平（\( x \)方向）に\(0.5 \) \( \rm m/s \)の初速度で投げ出したときの\(x-y\)平面内のボールの軌跡を計算し、アニメーション表示させることを考えてみます。重力加速度は\( y \)方向下向きに\( 9.80665 \) \(\rm m/s^{2}\) が作用しているものとします。

ボールの運動を追跡するには、Newtonの運動方程式を使います。
Newtonの運動方程式は時間に関する二階微分の形をとるので、数値解を得るには、初期条件(時間\( t ＝０\)での初期位置と初期速度という\(２\)個の情報が必要です。

Newtonの運動方程式から、速度の時間変化率（＝加速度）がわかり、変化率がわかれば適当な時間刻み幅\( dt \)を掛け算してやれば、現在の速度の状態から、オイラーの前進解法によって次の時刻における速度が求まります。さらに、速度は位置座標の時間変化率であるので、位置座標は現在の位置座標から、やはりオイラー前進解法によって次の時刻における位置座標が求まります。皆さんがボールを投げたときに目で追いかけているものは、この位置座標です。

数値計算をした結果は、皆さんが観察できる位置座標をアニメーションで表示することで、いつも目にしている内容と合っているか判定をすることができ、数値計算が妥当であることを確認しやすくなります。

下記に、計算を行い、そレから得られる位置座標をアニメーション表示するPythonプログラムの例を示します。

このプログラムの構造は、当研究所のブログでよく使うことになりますので、頭に入れておくとよいでしょう。

Jupyter Notebookで実行した結果の様子を以下に示します。
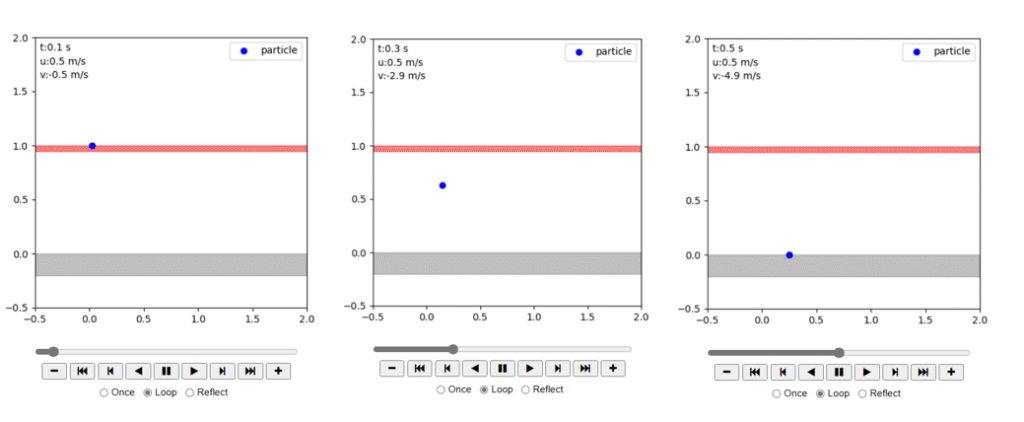
水平に投げ出されたボール（質点）は、水平方向には力が作用しないので等速度運動、鉛直方向には下向きに作用する重力によって下向きに加速されていきます。地面がないとそのまま落ちていくのですが、ここでは地面（\( y =0 \)) に到達したら、地面に沿って初速度のまま水平に移動する様子がわかります。地面でのボールの跳ね返りはないものとしています。
実際にはボールと地面の間には転がり抵抗や摩擦抵抗が水平方向にボールの進行方向とは逆向きに作用し、ボールを減速させ、やがて静止しますが、ここではそのような作用は入れていないので、いつまでも転がり続けます。
この話を聞いた時、次の二つの反応をとると考えられます。一つ目は、実際とは違うのでこの計算は役に立たない、もう一つは、実験では影響を取り除くのは難しいが数値計算は仮定を設定することで「もしもそのようなものがないとしたら結果はどうなるか」ということを検討できるのですばらしい、というものです。どちらの反応も「才能あり」ですが、その後、何をするかで真の価値が生まれます。一つ目の反応をした人は、この数値計算を実際に即した内容に改善する策を検討する、二つ目の反応をした人は、そのような検討の結果、実際とはいったい何であるのかを深く検討する、といったことに進むとよいのではないかと思います。両者とも、「実際」とは何かを深く理解することにつながります。そうすることで、真の理解を目指せることになります。

Newton力学の先に一般相対性理論があります。
もしも私たちが光の速度に近い生活をしているとしたら、一般相対性理論は小学生でも理解できます。その小学生がもしも速度が非常に遅いときにはどのようなことになるのかを検討してみると、Newton力学を発見するということになっていたわけです。